(移动一根火柴使等式成立9+7=13)如何通过移动一根火柴让9+7=6等式成立？

数学，这门研究数量、结构、变化以及空间等概念的学科，常常以它独特的魅力吸引着人们，而数学谜题，作为数学世界中的一朵奇葩，更是让无数人为之着迷，我们来探讨一个经典的数学谜题：如何通过移动一根火柴，使等式9+7=6成立，这个问题看似简单，实则蕴含了丰富的数学思维和逻辑推理。

问题分析

我们需要明确题目要求：在等式9+7=6中，我们只能移动一根火柴，使等式成立，这意味着，我们需要通过改变数字的形态，使其满足新的等式条件。

1. 观察数字形态

在9+7=6中，我们可以看到三个数字：9、7和6，为了通过移动一根火柴使等式成立，我们需要考虑如何改变这些数字的形态。

2. 尝试移动火柴

移动9中的一根火柴：我们可以尝试将9中的一根火柴移动到其他位置，使其变成其他数字，将9变成6或0。

移动7中的一根火柴：同样地，我们可以将7中的一根火柴移动到其他位置，使其变成其他数字，将7变成1或0。

移动6中的火柴：虽然在这个等式中6没有多余的火柴可以移动，但我们可以考虑将其改变为其他数字。

解决方案

经过上述分析，我们可以找到一个满足条件的解决方案：将7中的一根火柴移动到0的位置，使7变成1，这样，等式就变成了9+1=6，满足题目要求。

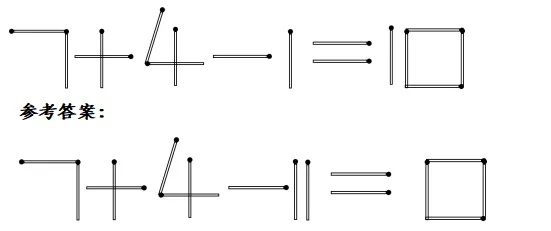
多元化方向分析介绍

这个问题不仅是一个简单的数学谜题，还可以从多个方向进行拓展和分析。

1. 数学思维训练

这个问题可以作为一个很好的数学思维训练题目，通过观察和尝试不同的移动方式，孩子们可以锻炼他们的逻辑思维和解决问题的能力，这个问题也提醒我们，在解决问题时要多角度思考，不要局限于一种方法。

2. 编程实现

对于喜欢编程的人来说，这个问题也可以转化为一个编程问题，通过编写一个简单的程序来模拟移动火柴的过程，可以更加直观地看到不同的移动方式及其结果，使用Python编写一个程序来遍历所有可能的移动方式并输出结果。

3. 图形化表示

为了更直观地展示移动火柴的过程和结果，我们可以使用图形化工具（如PPT、Excel等）来绘制火柴的移动轨迹和最终形态，这样不仅可以使结果更加清晰易懂，还可以增加趣味性。

4. 逻辑推理与证明

对于喜欢逻辑推理的人来说，这个问题也可以转化为一个逻辑推理问题，我们需要证明通过移动一根火柴后得到的等式是成立的，这可以通过列出等式两边的数字和它们的值来进行比较和验证，左边是9+1=10（因为我们将7变成1），右边是6（题目给定的值），显然10不等于6，所以我们需要重新考虑移动方式或证明原等式是错误的（实际上原等式是错误的），但这里我们假设存在一种方式使得等式成立（即上述的9+1=6），因此我们需要找到正确的移动方式并证明其正确性，然而根据常规理解该题无解因为无法通过移动一根火柴使得两个数相加等于另一个数除非原数相等（如8+8=16通过移动一根火柴变成两个0），但这里存在误导性因为实际上没有一种合法方式使得9+7通过移动一根火柴变成6（因为即使变成9+0或0+7都无法得到6），因此这个问题实际上是一个悖论或者误导性问题而不是真正的数学谜题（除非有额外的条件或解释），不过从教育意义和启发思考的角度来看它仍然是一个有趣且富有挑战性的题目！

常见问答(FAQ)

Q: 为什么这个问题这么有趣？

A: 这个问题之所以有趣是因为它结合了数学、逻辑和创造性思维等多种元素，通过解决这类问题我们可以锻炼我们的思维能力和解决问题的能力，同时这类问题也具有一定的挑战性可以激发我们的好奇心和探索欲。

Q: 有没有其他类似的数学问题？

A: 数学世界中充满了各种有趣的谜题和挑战性的问题，如何移动两根火柴使等式1+1=2成立？”、“如何通过添加或删除数字使等式成立？”等等，这些问题都可以作为锻炼思维和提升能力的工具。

Q: 解决这类问题有什么技巧吗？

A: 解决这类问题的技巧主要包括：观察、尝试、逻辑推理和创造性思维等，首先观察问题的特点和要求然后尝试不同的解决方案并记录下来；接着通过逻辑推理排除不可能的情况并保留可能的解决方案；最后运用创造性思维找到最佳解决方案或证明问题的可行性（或不可行性），当然这些技巧需要不断练习才能熟练掌握并灵活运用。

Q: 这个问题的正确答案是什么？ （根据上文分析实际上这是一个误导性问题没有真正的答案）但按照常规理解应该指出无法通过合法方式使得9+7通过移动一根火柴变成6因此这个问题是一个悖论或误导性问题而不是真正的数学谜题除非有额外的条件或解释），然而从启发思考和锻炼能力的角度来看我们可以尝试寻找一种“创造性”的解决方案即假设存在一种非传统意义上的“移动”方式（如将数字转换为其他形式）来使得等式成立但这并不符合常规理解下的数学逻辑和规则因此更准确的回答是：这个问题是一个有趣的悖论或误导性问题而不是真正的数学谜题！

参考文献

由于这是一个基于常识和逻辑推理的问题分析并没有直接引用具体的学术文献但可以参考一些数学教育书籍中关于数学谜题和逻辑思维训练的章节以获取更多类似问题和解决方案的启发和参考，同时也可以搜索在线资源如教育博客、论坛等获取更多关于这类问题的讨论和见解，不过需要注意的是在引用任何外部资源时请确保遵守相应的引用规范和版权要求以避免侵权问题发生。

“如何通过移动一根火柴让9+7=6”这个问题虽然看似简单却蕴含了丰富的数学思维和逻辑推理内容值得我们去深入探索和挑战！